
GEOMETRIC CONTROL OF QUADROTORS FOR AGGRESSIVE MANEUVERS
Summer 2020
Boston University Robotics Lab
PROJECT DESCRIPTION
Aerial robotics are used for a wide variety of applications. This research project focuses on improving quadrotors for usage in law enforcement search and rescue missions, but can be applied universally to any situation. The most commonly used quadrotor controllers combine an open-loop control planner with a closed-loop feedback that assumes the quadrotor is always near the hover state. This control method can follow trajectories under near perfect conditions. The biggest issue with this method is that a quadrotor cannot recover from large variations (i.e. a strong gust of wind) that causes it to leave the hover state. The quadrotor will be thrown off course, resulting in a crash.
This project will focus on implementing a geometric closed-loop controller on quadrotors. Professor Tron and his graduate students have ran theoretical simulations and published research that shows that their controller should work better than traditional controllers. However, the new controller has yet to be proven in practice. My role on this project will be to run experiments testing the controller on quadrotors to prove that the new controller does indeed work better. I will be participating on the project remotely, connecting with my lab group on a weekly Zoom call.
WEEK 1
The goal of this week was to set up my software and simulation environment. I purchased an HP 5.6 Touch-Screen Laptop-AMD Ryzen 5 and erased the existing Windows software. Using a USB-stick, I downloaded the software Ubtunu 18.4 onto it and reinstalled Ubtunu onto the laptop, converting my Windows laptop to a Linux system. Afterwards, I downloaded and installed the programs Gazebo, Robotic Operating System (ROS), MATLAB, and PX4 and made sure they ran correctly. Week 1 was a pleasant challenge because it was the first time I worked solely with a Linux system. There was a small learning curve in adapting to Linux, but online documentation was incredibly helpful.
WEEK 2 & 3
The goal for these weeks was to become comfortable and understand the code for a linear double integrator system in MATLAB. The purpose of the double integrator code is to model how a geometric controller behaves when you manipulate its proportional (KD) and derivative (KV) error gains. In a quadrotor the proportional error gain (KD) is used to minimize the tracking error, which means it's responsible for adjusting to any changes introduced. The derivative error gain (KD) is used fo dampening, which means it works to reduce high and medium level frequency vibrations while allowing low level frequencies to be registered. Playing around with gain values revealed many interesting patterns which are further discussed in the section below.
WEEK 4
The goal of this week was to set up this blog/portfolio with my current work. That included setting up this page, recording my past weeks milestones, and delving deep into the double integrator system so that I could accurately explain my findings. I found myself looking up articles on PID controllers to supplement my understanding, and found a lot of benefit it thoroughly documenting my research. It helps me make sure I understand what we are doing by writing it in my own words.
On Wednesday, June 24th I paused my work to partake in BU's Day of Engagement to Discuss Racism. It was an insightful day full of conversations, a roundtable lunch, and open honesty from members within the BU community and out about the effects of racism on fields as wide as STEM. I learned a lot about my own unconscious bias and realized I have a lot to learn about the history of our country. I especially enjoyed the conservations at the end of the day that focused on how to partake in antiracist work, especially in the STEM field. I feel like there is much work to do in creating a just playing field for everyone in STEM, and am excited to contribute in a change.
Later in the week, I worked on creating a 3-D animated graph but found it difficult animating the vectors. I will ask for help and then attach the video in the double integrator system section below. I also began to work withe ODE45 system to look for the acceleration and torque by feeding in x to find the states.
WEEK 5
I began this week by quickly re-running through the MATLAB double integrator tests, setting each test to the same initial position and velocity. I then began working on going through the quadrotor Matlab controller. It was a bit complicated so I held off on that for a bit so I can find time to meet with Bee. I also updated the BU Robotics Lab Wiki with the most up to date information. Moving forward, I began working with the Pixhawk Odriod. I followed the instructions on BU Robotics Wiki to install the Pixhawk Odriod system onto my Linux laptop. Following this page allowed me to begin working with the Pixhawk Odriod using Robotic Operating System (ROS) to command the controller to move to different waypoints.
DOUBLE INTEGRATOR SYSTEM
The double integrator system is a linear system that has two error gains, the proportional (KD) gain and the derivative (KV) gain. Manipulating these two gains affects the position and velocity of the point mass, thus making this system a good model for the non-linear quadrotor controller. The proportional error gain represents position, or how fast the point mass takes to reach its final state. The error part is responsible for reacting and making adjustments to the point mass's position to stay on course. The derivative error gain represents velocity, or how long it takes for the point mass to reach its destination. The error part in that represents how fast the controller can dampen the oscillations until they reach zero. Dampening the oscillations means the control is reducing high-medium frequency vibrations and only allowing lower level frequencies through. The tests run below play around with these error gains, manipulating their values to reveal what occur in different scenarios if one gain were to be too large etc.
All of these tests are set to the same initial position and velocity.
x0_pos = [-2; 3.5; 15]; position
x0_vel = [-3; 7; 19]; velocity

SIMILAR ERROR GAINS
In this test, the proportional and derivative gains are set to values very close to one another. As result of, the
plot shows large to mild oscillations that decease to zero after some time. The oscillations in this graph versus some of the others are unique because they are spread out, showing that it took quadrotor some time to stabilize before reaching its desired position.
Closed Loop Eigenvalues:
-1.0000 + 1.4142i
-1.0000 - 1.4142i
Proportional Gain (KD) = 3
Derivative Gain (KV) = 2

LARGE PROPORTIONAL (KD) GAIN
In this test, the proportional (KD) gain was set to a large value and the derivative gain was set to a small value. As a result of, the plot shows oscillations all the way until it eventually reaches zero. Because the proportional gain was so large, it overpowered the dampening effect of the derivative gain; the oscillations in the graph are actually the quadrotor overshooting its desired position rapidly until it eventually reaches its desired spot. similarly, because the derivative gain is so low, it takes almost double the time to reach zero than any other test.
Closed Loop Eigenvalues:
-1.0000 + 3.7417i
-1.0000 - 3.7417i
Proportional Gain (KD) = 15
Derivative Gain (KV) = 2

LARGE DERIVATIVE (KV) GAIN
In this test, the derivative (KV) gain was set to a large number and the proportional gain was set to a small value. As a result of, the plot displays critically damped curves that reduce to zero after some time. There are no oscillations in this graph which means the derivative gain completely overwhelms the proportional gain. In a quadrotor controller, a large derivative gain means that the quadrotor will reach its desired position quickly, but doesn't account for position accuracy.
Closed Loop Eigenvalues:
-0.2027
-14.7973
Proportional Gain (KD) = 2
Derivative Gain (KV) = 15

SAME ERROR GAINS
In this test, both proportional and derivative gains were set to the same value. As a result of, the plot displays large oscillations within the first fifteen seconds which then reduces to zero after some time. The initial oscillations show that the quadrotor attempts to move into position but because the position and velocity are set to the same values it quickly reaches its final position. There is not much position accuracy when the gains are set to the same value.
Closed Loop Eigenvalues:
-1.3820
-3.6180
Proportional Gain (KD) = 5
Derivative Gain (KV) = 5

WHEN THE PROPORTIONAL (KD) GAIN IS 0
In this test, the proportional gain was set equal to zero, representing no position accuracy. As seen in the plot, the derivative gain sets the time it takes for the point mass to reach its final state, and without any position the point mass never reaches zero. It's like the quadrotor moves in one direction endlessly because it does not know where to stop.
Closed Loop Eigenvalues:
0
-2
Proportional Gain (KD) = 0
Derivative Gain (KV) = 2
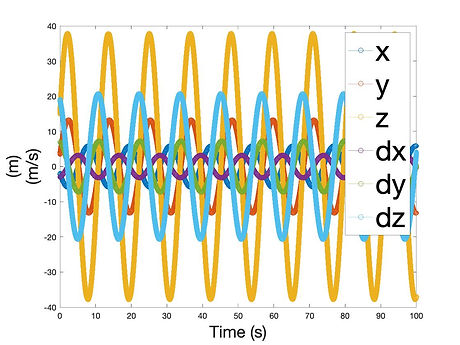
WHEN THE DERIVATIVE (KV) GAIN IS 0
In this test, the derivative gain is set to zero, representing no velocity in the system. As seen in the plot, the proportional gain oscillates endlessly, never reaching its final state. There are both large and small oscillations, indicating that the system deviates wildly from its desired position. It's almost like the quadrotor is hovering endlessly, never knowing when to stop.
Closed Loop Eigenvalues:
0.0000 + 1.7321i
0.0000 - 1.7321i
Proportional Gain (KD) = 3
Derivative Gain (KV) = 0
QUADROTOR ATTITUDE CONTROLLER
The quadrotor attitude controller

SIMILAR ERROR GAINS
In this test, the proportional and derivative gains are set to values very close to one another. As result of, the
plot shows large to mild oscillations that decease to zero after some time. The oscillations in this graph versus some of the others are unique because they are spread out, showing that it took quadrotor some time to stabilize before reaching its desired position.
Closed Loop Eigenvalues:
-1.0000 + 1.4142i
-1.0000 - 1.4142i
Proportional Gain (KD) = 3
Derivative Gain (KV) = 2

LARGE PROPORTIONAL (KD) GAIN
In this test, the proportional (KD) gain was set to a large value and the derivative gain was set to a small value. As a result of, the plot shows oscillations all the way until it eventually reaches zero. Because the proportional gain was so large, it overpowered the dampening effect of the derivative gain; the oscillations in the graph are actually the quadrotor overshooting its desired position rapidly until it eventually reaches its desired spot. similarly, because the derivative gain is so low, it takes almost double the time to reach zero than any other test.
Closed Loop Eigenvalues:
-1.0000 + 3.7417i
-1.0000 - 3.7417i
Proportional Gain (KD) = 15
Derivative Gain (KV) = 2

LARGE DERIVATIVE (KV) GAIN
In this test, the derivative (KV) gain was set to a large number and the proportional gain was set to a small value. As a result of, the plot displays critically damped curves that reduce to zero after some time. There are no oscillations in this graph which means the derivative gain completely overwhelms the proportional gain. In a quadrotor controller, a large derivative gain means that the quadrotor will reach its desired position quickly, but doesn't account for position accuracy.
Closed Loop Eigenvalues:
-0.2027
-14.7973
Proportional Gain (KD) = 2
Derivative Gain (KV) = 15

SAME ERROR GAINS
In this test, both proportional and derivative gains were set to the same value. As a result of, the plot displays large oscillations within the first fifteen seconds which then reduces to zero after some time. The initial oscillations show that the quadrotor attempts to move into position but because the position and velocity are set to the same values it quickly reaches its final position. There is not much position accuracy when the gains are set to the same value.
Closed Loop Eigenvalues:
-1.3820
-3.6180
Proportional Gain (KD) = 5
Derivative Gain (KV) = 5

WHEN THE PROPORTIONAL (KD) GAIN IS 0
In this test, the proportional gain was set equal to zero, representing no position accuracy. As seen in the plot, the derivative gain sets the time it takes for the point mass to reach its final state, and without any position the point mass never reaches zero. It's like the quadrotor moves in one direction endlessly because it does not know where to stop.
Closed Loop Eigenvalues:
0
-2
Proportional Gain (KD) = 0
Derivative Gain (KV) = 2

WHEN THE DERIVATIVE (KV) GAIN IS 0
In this test, the derivative gain is set to zero, representing no velocity in the system. As seen in the plot, the proportional gain oscillates endlessly, never reaching its final state. There are both large and small oscillations, indicating that the system deviates wildly from its desired position. It's almost like the quadrotor is hovering endlessly, never knowing when to stop.
Closed Loop Eigenvalues:
0.0000 + 1.7321i
0.0000 - 1.7321i
Proportional Gain (KD) = 3
Derivative Gain (KV) = 0